On-chain Procedural Generation ​

by Nalin and gubsheep. With gratitude to Alan Luo from Dark Forest for introducing us to the concept and providing us many educational resources.

Over the past two years, teams in the 0xPARC community have been exploring experimental techniques for crypto-native gaming, building primitives for "autonomous worlds" on top of blockchain technology. In this post, we'll talk about on-chain procedural generation, a technique used by Dark Forest, Lattice, and exgrasia.

Procedural generation allows us to create rich worlds (landscapes, dungeons, castles, clouds…) programmatically by the use of expressive but inexpensive algorithms that can be run on the blockchain. Procedural generation algorithms typically attempt to emulate natural world formation processes, embedding variety and realism in the pseudorandomness of their outputs.

In this post, we'll explain why and how you would start implementing such algorithms on-chain. You can check out a demo repo here--different branches show different stages of development of a simple world generation algorithm.

Why do we use procgen? ​

Players often want rich and immersive worlds to interact with. Knowing this, your first instinct as a game developer might be to build your game world block by block - by hand. Off chain, handmade maps are extremely commonplace - games like DayZ and Fortnite carefully engineer detailed towns and hills optimizing for maximum fun.

On-chain, however, we deal with a big constraint - storage cost. Storing a single 32-byte word on Ethereum can cost over 20,000 gas (EVM gas schedule). It would be infeasible to store even a 1000x1000 2D tilemap on chain; larger maps could require thousands (or even millions) of SSTORE operations, which is far more than can be done in a single EVM transaction given the block gas limit. Additionally, in many games, you don't actually want the whole world to be visible at the outset; for example, perhaps you want players to have to uncover the world through exploration over time.

The use of procedural generation allows you to generate each of these tiles on-demand, only writing to storage when a player first interacts with a particular coordinate. Each individual call to a procedural generation algorithm (Perlin Noise, for instance) can be fairly cheap - in our very unoptimized demo below, initializing an effectively infinite world is "free," while touching a tile and running the Perlin Noise algorithm for the first time costs about 70,000 gas. By running procedural generation and caching a tile’s attributes when someone first steps on it, you can amortize the cost of storing the map on-chain amongst all the players of your world. In some sense, a procedural generation algorithm is a trick to compress a complex world into an executable.

Procedural generation definitely isn’t a new idea specific to onchain gaming! Almost all your favourite roguelike games use procedural generation in some way or the other, including Minecraft (for landscape generation), No Man’s Sky (for planet generation) and Dwarf Fortress (for creatures, religions, etc.) among many others.

Procedural generation for world building is, unsurprisingly, a technique originally pioneered by games running on 16kb RAM and 1MHz processors back in the 90s (and earlier!). It’s interesting how many similarities there are between the resource-limited personal computers of the 90s and the resource-limited shared computer today that is the Ethereum Virtual Machine. In many ways, we’re in the 90s of crypto-native gaming, and developing an on chain world right now is an exercise in balancing constrained creativity and being resourceful and hacky with what’s possible with on-chain compute.

How do we use procgen? ​

So far, we’ve only described procedural generation in hand wavy terms - “make me a cool looking world.” How do we actually do this efficiently?

Randomly-generated assets ​

The simplest strategy is to simply "roll a die" (run a pseudorandom function) for every tile, planet, game asset, etc. Depending on how the roll comes up, you might choose to assign a different property value to the game object in question--for example, if a creature's hash ID ends in a 0, color it blue; otherwise, color it red. This is the easiest way to level up a game world beyond simply being a blank white slate.

In the earliest versions of Dark Forest, every coordinate had a 1/16384 chance of "spawning" a planet, and each planet would randomly be assigned a color, a level, and various stats. This variety gave players implicit goals--discover the rarest planet types, conquer a top-level planet, etc.

An early build of Dark Forest

Other early blockchain games like CryptoKitties also used relatively simple random generation methods to generate a large number of image assets cheaply. The properties of each digital cat are determined by an algorithm that is inexpensive to run; however, the number of possible trait combinations that you can roll is effectively infinite. This technique has since been copied by the thousands of speculative NFT clone projects that fueled the latest hype cycle.

While purely random generation is certainly better than nothing^[1], worlds and game assets generated randomly with no deeper coherence tend to start feeling stale relatively quickly. Without any notions of locality or progression, gameplay quickly degenerates into pulling a slot machine lever. Zooming out in a universe of randomly-generated assets, everything starts to looks like white noise.

Structure from Randomness ​

As a next step, what we'd like is a way to convert pure randomness into something with recognizeable "structure" - a source of entropy that feels random, but also isn’t completely chaotic to look at. More formally, our aim is to create a noise function that is variant when looked at globally, but locally consistent zooming in. To understand the intuition to making such a function, let’s start with something fundamental: sine waves! As a quick refresher, a sine wave is an equation that looks like $$y = amplitude * sin(x * frequency)$$. Amplitude and Frequency parameters allow you to squish or stretch the wave horizontally and vertically.

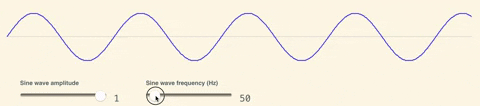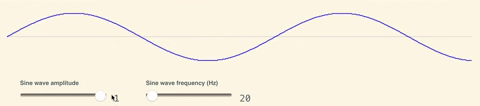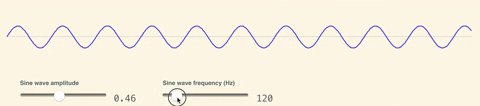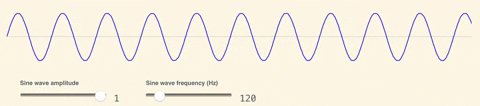
Another interesting concept is super-position: the ability to add up different wave functions. See what happens when we add up many sine waves with random parameters:

You can also play around with these waves interactively in this Observable notebook.

We get a lot more variation in our output globally, while maintaining the local similarity property we desired. This is how procedural generation works! Formally, each of the constituent waves is called an “octave”, each adding more complexity to the surface of the output.

Instead of using a sine wave, Perlin Noise uses a different function. While it follows the same idea, it's less regular compared to sine waves and its amplitude is more consistent. While it is technically possible to build all the generations we describe below with simple trigonometric functions like sine waves, Perlin noise is easier (and prettier) to use, so we’ll focus on Perlin Noise going forward.

How does Perlin noise work? ​

Before we start exploring worldly Perlin structures, we’ll introduce one more idea of procedural generation: dimensionality. In the previous section, we’ve only worked with one dimensional waves — how can we extend this idea to 2D maps (or for that matter, N-dimensions)? Primarily, we now have to maintain the notion of regularity across not just one, but two dimensions.

The core idea of Perlin can be summarised as follows: take your 2D grid and break it into chunks (of say, size 5 x 5). Next, put random vectors at the corners of each chunk. Next, to compute the noise function at any (x, y) coordinate, obtain the random vectors at the corners of the chunk, and interpolate between them - this is just a fancy way of saying “compute a smoothened value that translates between the random vectors at the corners” using some calculus. There are some tricks to making a clean/clever interpolation between the vectors, but those are not particularly important for this discussion.

Credits: UMD CMSC 425

Assigning greyscale color values on a sample 2D map using this process might give us something like this:

Creative world building with Perlin Noise ​

The image above shows some elements of randomness and some elements of local structure simultaneously. However, it's a far cry from a rich game world map.

For a first step, let's assign tile types to coordinates by chopping up the range of possible Perlin values into "intervals." We'll interpret Perlin values as atlitudes relative to sea level: tiles with low Perlin values will be labeled as water tiles; successively higher perlin values will be labeled as sand (for beaches), then forest, then stone, the snow (for mountaintops).

Now we're getting somewhere! This is starting to look a bit more like a world. One could imagine a player making a long journey through a forest, fishing at the coastlines, and scaling an imposing mountain range to reach a dungeon.

We'll make one more modification to our Perlin algorithm. In the picture above, the landscape is kind of "blobby"--all geographic features exist on roughly the same scale. Below, we build a "multi-octave" Perlin function by adding together Perlin functions with different frequencies and amplitudes, in a way that is spiritually similar to the "super-position" idea mentioned above for trigonometric functions.

In this iteration, we see that landscape features exist at multiple different scales. There are large and small bodies of water, and there are tiny "outcrops" that jut out from coastlines that are otherwise smooth.

Now that we have a simple landscape resembling some sort of archipelago, let’s look at ideas that bridge this to more interesting world maps. For starters, what if we built something resembling our own world - with a North Pole at the top and more tropical/equatorial regions as me move downward from the Pole. We already have a notion of height of a tile. We essentially want to add a temperature parameter to our tile, one that while being somewhat random, follows the pattern we observe in the real world. To imbue this pattern, we’ll cleverly super-position perlin output with a simple linear function of our own:

temperature += Math.floor((coords.x - 50) / 2);

By taking our old sine-wave-esque function and adding a linear function to it, we can retain the rough pattern we desired, along with the realistic landscape features. Now, we can use this temperature value in conjunction with height to switch tile types:

 function seedToTileType(
        Coords memory coords,
        uint256 perlin1,
        uint256 perlin2
    ) internal pure returns (TileType) {
        uint256 height = perlin1;
        uint256 temperature = perlin2;
        temperature = uint256(int256(temperature) + (int256(coords.x) - 50) / 2);

        AltitudeType altitudeType = AltitudeType.SEA;
        if (height > 40) {
            altitudeType = AltitudeType.MOUNTAINTOP;
        } else if (height > 37) {
            altitudeType = AltitudeType.MOUNTAIN;
        } else if (height > 32) {
            altitudeType = AltitudeType.LAND;
        } else if (height > 30) {
            altitudeType = AltitudeType.BEACH;
        }

        TemperatureType temperatureType = TemperatureType.COLD;
        if (temperature > 42) {
            temperatureType = TemperatureType.HOT;
        } else if (temperature > 22) {
            temperatureType = TemperatureType.NORMAL;
        }

        TileType tileType = TileType.UNKNOWN;
        if (temperatureType == TemperatureType.COLD) {
            if (altitudeType == AltitudeType.MOUNTAINTOP) {
                tileType = TileType.SNOW;
            } else if (altitudeType == AltitudeType.MOUNTAIN) {
                tileType = TileType.SNOW;
            } else if (altitudeType == AltitudeType.LAND) {
                tileType = TileType.SNOW;
            } else if (altitudeType == AltitudeType.BEACH) {
                tileType = TileType.SNOW;
            } else {
                tileType = TileType.WATER;
            }
        } else if (temperatureType == TemperatureType.NORMAL) {
            ...
            // less snow, more grass
        } else {
            ...
            // less grass, more sand
        }
        return tileType;
    }

With this set of patches, we obtain this nice, earthly map:

Code. Notably, this is also the exact map used by exgrasia.

It is also really simple to derive new maps by just being a little creative with color schemes and perceptions. This exact map with some changes can be seen as a Minecraft nether-like map, for instance:

Code.

To create these previous two maps, we’ve used plain x-coordinates to imbue a cool, globally emergent property to our procedurally generated temperature value - lower x coordinate cells are colder than higher x coordinate cells. What if we assigned temperature based on distance from centre of the map? Let’s try it:

Code.

We obtain an island with a mountain at the centre surrounded by snowy lands and a beach at the edges. And perhaps, if you run with imagination, it looks like the snowy area is a sideways portrait of a smiling ghost.

Let’s take this idea one step further. Instead of thinking about our map in a Cartesian plane, what if we look at it in the polar coordinate system? As a quick reminder, polar coordinate systems demarcate points by their distance from the origin and the angle between the line from origin to the point with the x axis. Here’s what happens if we use this coordinate system as the basis of generation:

Code.

We obtain a map with much more radial symmetry. This is not surprising - we’ve essentially unrolled a rectangular map into a series of concentric rings to obtain this map! Perhaps this map is also somewhat reminiscent of the map of the city of Amsterdam! A city built around concentric rings of buildings and canals (and where the latest Devconnect was hosted).

Putting worlds on-chain ​

So far, this blog has focused on the use cases for Perlin noise and procedural generation in making pretty maps. But how do we put these worlds on-chain? In fact, all the generations described above have accompanying solidity implementations - if you checkout the linked branches locally and right click any tile, you should see console logs verifying the generated tile types between the solidity and javascript versions - and you can find the generating code in eth/contracts/TinyWorld.sol. All Perlin code is neatly self-contained in the library Perlin.sol that you can export to your own projects.

Thanks to the DarkForest team, there’s also a ZK circuit that can compute and verify Perlin Noise generations that may be relevant to readers.

Whackier ideas ​

As you explore the world of procedural generation further, here's some of my own favourite advanced uses of procedural generation:

• Put it in a SNARK!: To build a rich universe with multiple biomes hidden behind a fog of war, Dark Forest implements the Perlin Noise function in a circom SNARK circuit, rather than in Solidity.
• Fractal Brownian motion: The creation of maps that recursively use the output of Perlin Noise to create more noise - kind of like taking the aforementioned rectangular/polar coordinate systems described in our Amsterdam exploration and replacing those by a coordinate system itself defined by Perlin Noise.

• Perlin Planets: The creation of force fields to make continuous spherical maps is super neat! Dark Forest also uses a variety of procedural generation tricks to render rich and visually unique planets.

• Volumetric clouds: Creating convincing looking moving cloud skyscapes efficiently is a hard task! While there's a lot of (noisy) details to the complete generation method, it, too, builds on Perlin Noise!

Where do we use procgen? ​

It’s funny how on one hand crypto-native games feel like this unscratched surface with seething potential to change how we think about games at all, and yet, these are such early days that some of the best on-chain games right now only require algorithms simple enough to describe in blog posts like this one. Constraints breed creativity, and we hope this blog inspires you to go explore affordances of the blockchain by building your own crypto native game - regardless of how basic it might feel. Perhaps the biggest trap right now amongst crypto-native gaming devs is to fall into the trap of being over ambitious and running L1s for land NFTs and tokenomics and what not. KISS.

Credits ​

If you found this interesting, you may also find it interesting to explore and/or build tile contracts on top of exgrasia, which started with explorations of this form of on-chain procedural generation!

This is a more polished version of a talk gubsheep and Nalin gave at D.E.F CON. The concept was originally introduced to us by Alan Luo, an early Dark Forest core team member, who used procedural generation heavily in building the Dark Forest renderer and suggested Perlin Noise as a candidate algorithm for putting in a SNARK. The solidity implementation of Perlin Noise was originally written by gubsheep, and the zk-SNARK circuit implementation was written by Robert Cunningham, another early member of the Dark Forest team. Thanks also to Yush, with whom the first explorations of the exgrasia landscape were made.