Group Signatures with zkSNARKs ​

a demo by Joel G, Matt Katz, Uma R, Kevin Z, Raymond Z, and gubsheep

zkSNARKs turn cryptography problems into programming tasks. The programmability of zkSNARK circuits allows them to emulate and extend a wide variety of cryptographic primitives which previously required the construction of new mathematical protocols. In this post, we break down a basic zkSNARK construction that implements an old cryptographic primitive—the “group signature scheme.” We also demonstrate a proof-of-concept implementation of an anonymous message board based on this scheme.

Introduction ​

In many online communities, allowing members to participate with both credibility and anonymity seems paradoxical. Your reputation is closely linked with your identity—how can you verify the credibility of a statement coming from an untraceable source?

On the one hand, anonymity allows "anons" and "throwaway accounts" on platforms like 4chan and Reddit to speak their minds in ways that they might not otherwise be comfortable with, and enables whistleblowers to publicly disclose corporate or government wrongdoing while protecting themselves from retaliation. On the other hand, it's difficult to verify the credibility of statements that are not attached to known or trusted identities, and complete anonymity can be a tool for bad actors who wish to spread misinformation or harass other community members. Ideally, we'd like to enable participants in high-stakes discussions to prove their credibility without giving up their privacy.

Enter group signatures. In a cryptographic group signature scheme, participants can generate message signatures that prove their membership in a known set of actors, without revealing their specific identity. The Federalist Papers are a historical example of group signatures in action—essays were signed by ”Publius,” a group pseudonym for Alexander Hamilton, James Madison, and John Jay (h/t Dan and Varun).

In this post, we'll demonstrate a few techniques for implementing easy-to-write group signatures using zkSNARKs (about 40 lines of circom code!). These group signature SNARKs can be plugged in to webapps, integrated with identity providers (Ethereum accounts, social media accounts, and more), and augmented with a variety of optional properties like traceability, deniability, and more.

Notably, using zkSNARKs turns augmentation and configuration of group signature protocols into a programming task, rather than a math problem. For example, instead of having to invent a whole new cryptographic mechanism to enable the property of "deniability," you can just add or modify a few lines of ZK circuit code. Our group signature demonstration is just one example of a broader pattern—zkSNARKs enable developers to program new cryptographic primitives, without having to think about elliptic curves, bilinear pairings, polynomial commitments, or other crypto math.

Proof of Concept: ZKMessage ​

Practical group signature schemes have many interesting use cases. A cryptopunk holder, or a Twitter user with 1M+ followers, can post anonymous messages with signatures that prove those respective properties but reveal nothing else about their identities. Further out, one could imagine a high-level politician using group signatures to anonymously signal support for proposed legislation during consensus-building prior to a public vote, maintaining their privacy to avoid short-term political backlash while proving their membership in a party or the legislature.

As a simple proof of concept, we built ZKMessage: a message board that allows users to generate anonymous group signatures. Try it out for yourself here!

Users first claim a ZKMessage public key by Tweeting an attestation to a freshly-generated keypair. When a user wishes to submit a post, they select up to 39 other users to form a group, generate a group signature ZK proof for their message client-side, and then send the message and signature to our server, which stores signed posts in a Postgres database. The webserver then serves these signed posts to users who wish to view the message board; users can verify signatures client-side, though they won’t be able to narrow down the original poster beyond the poster’s specified group.

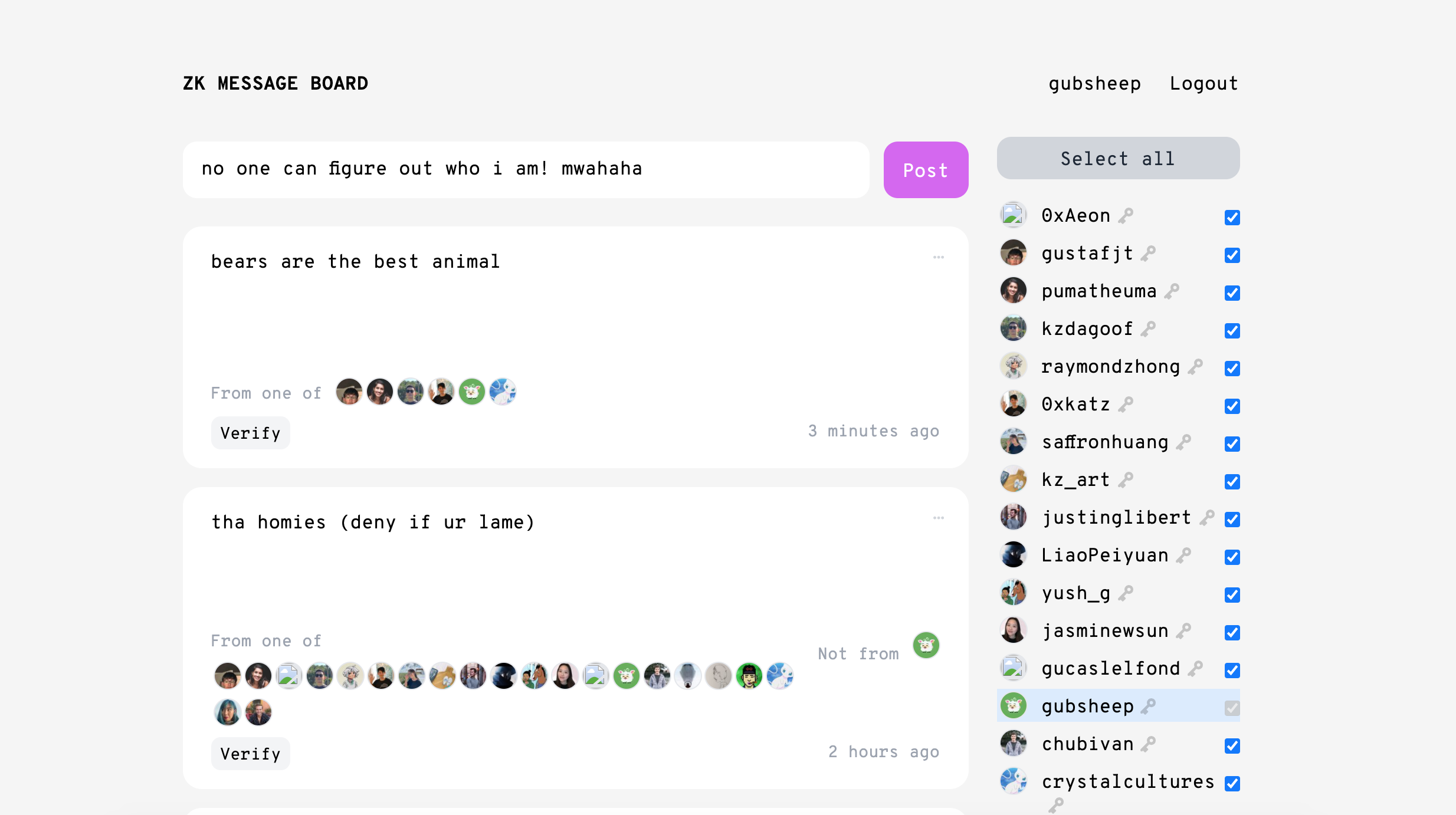
ZKMessage has the following properties:

• Group signatures are unforgeable. No one can sign a message on behalf of a group of which they are not a part.
• Group signatures provide cryptographic anonymity. For any given group-signed message, no one (except the signer) can figure out who in the group produced the message.
• Messages and signatures can be censored (though this can easily be fixed). Because posts are stored and served by a centralized agent—our webserver—the server can refuse to serve a post. This centralization isn’t necessary for the protocol, however; you could eventually swap out the server for a decentralized data layer (i.e. a smart contract or p2p network).

ZKMessage is for demonstration purposes only. We will disable the ability to post at some point in the near future, and we’ll remove any offensive / bad-faith posts.

We hope that this demonstration may hint at further applications—we’ll discuss potential extensions to digital voting systems, privacy-preserving authentication systems, and more below—but much work remains to be done. You can find the ZK circuit code here, and the webserver / frontend client code here.

Background ​

Group Signatures ​

Group signatures are an old and fairly well-studied cryptographic primitive. Constructions for group signatures have been around for decades, dating back to Chaum and Van Heyst's initial paper from 1991. Different group signature schemes vary along several dimensions and provide different guarantees:

• Does the group need to be fixed in advance? Some schemes require the group to be declared in advance, with a group-specific setup process (sometimes even requiring a trusted group manager). Other schemes are dynamic, allowing groups to be generated on the fly for each signature (see ring signatures) given a known addressbook.
• Can the scheme allow for a trusted entity (or entities) with additional permissions? For example, some schemes allow for a trusted group coordinator who can't forge signatures, but who can undo the anonymity of a signature using a trapdoor (traceability).
• Can a participant confirm that a previously-generated group signature was indeed signed by them individually, without revealing their secret key?
• Can a participant deny a group signature, proving that they were not the one who signed the message, without revealing their secret key?
• How long (in bits) must signatures be to achieve a desired level of security? Does the length of the signature vary with the size of the group?

Plenty of theoretical work has been done to invent protocols with various different properties, asymptotic efficiencies, etc.^[1] However, as far as we can tell from a cursory overview, these protocols haven't found too much real use in practice^[2], despite the fact that there are many "obvious" potential applications. Our hope is that zkSNARK tooling might make programmable group signatures easier to implement and integrate into dapps, potentially unlocking some applications which couldn't have on their own justified implementation of an entire cryptographic signature scheme (and toolstack) from scratch.

zkSNARKs ​

zkSNARKs are a powerful new tool that allows you to prove that you've correctly executed some publicly-known code on a secret input, and obtained some publicly-claimed output as the result of the computation. If you aren't familiar with SNARKs, you can read more about them here.

zkSNARKs are powerful because they allow us to generate zero-knowledge proofs for any mathematical function.

In the example of digital signatures, previous generations of cryptographers had to create specific mathematical protocols to enable a ZKP for the secret key / public key relationship; that machinery can't be easily "reprogrammed" to build a ZKP for modular exponentiation, or SHA256, or the Dark Forest game's cryptographic fog of war mechanic. Similarly, each group signature scheme has historically relied on specific cryptographic machinery, and building a group signature scheme with a different set of properties might require starting from scratch and using different mathematical building blocks.

Conversely, zkSNARKs enable you to generate ZKPs for arbitrary code—allowing developers to program a "cryptography computer," without needing deep theoretical knowledge of the underlying mathematical machinery. To use a rough analogy: if inventing a new cryptographic scheme is like building an ASIC, writing a SNARK is like programming a Turing-Complete, general-purpose computer.

In the next sections, we'll show how SNARKs can enable "programmable" group signatures.

Circuit Construction ​

Our proof-of-concept ZKMessage circuits are written in Circom, a language used to define zero-knowledge protocols. We present three circuits: the first circuit (sign) is the most important, and is the only circuit that is strictly necessary to emulate a group signature protocol. The protocol can be augmented with revealSigner and denySigning circuits as add-ons.

1. sign: Attest to a message while proving membership in a group.
2. revealSigner: Prove that your specific secret key was used to sign a particular group-signed message.
3. denySigning: Prove that your specific secret key was not used to sign a particular group-signed message.

In our scheme, each user is identified by a public key, which is simply defined as the hash of the user’s secret key. Thanks to zkSNARKs, defining the public key as the output of a one-way function run on a secret key is sufficient for our purposes—we don’t need any other mathematical relationship between public and secret keys.

sign ​

Here's the high level outline of the message signing circuit:

**Inputs:**
- hash1, hash2, hash3, ... - public hashes of users in the group (public input)
- msg - Message to be broadcasted (public input)
- secret - User's secret key (private input)

**Outputs:**
- msgAttestation

The circuit needs to prove several things, that we will explain in detail below:

- myHash := mimc(secret)
- (myHash - hash1)(myHash - hash2)(myHash - hash3)... == 0
- msgAttestation := mimc(msg, secret)

We first take the user's secret and apply the MiMC hash (a SNARK-friendly hash) over it, deriving the public hash. We then take the user's public hash and compare it to the list of all public hashes that exist. Once we verify that the public hash does exist in this list, which means the user is a valid member of the group, we “sign” the intended message using the secret key and return it.

Circuit Breakdown ​

To demonstrate the circuit conceptually, we fix the number of input hashes to 3 although it can be arbitrary. We’ll break down snippets of example Circom code below; the full circuit can be found here.

We first declare a few inputs, one private and the rest public. hash1, hash2, hash3 are the public hashes of other users representing the group. secret is the sender's secret key, and msg is the message the user is attesting to.

The first portion of the circuit applies the MiMC hash to user's secret key and stores the result (the public hash) in the myHash signal.

component mimcSecret = MiMCSponge(1, 220, 1);
mimcSecret.ins[0] <== secret;
mimcSecret.k <== 0;
myHash <== mimcSecret.outs[0];

We then check that myHash, the MiMC hash of the user secret, is equal to one of the public hashes. If so, this means that the user is part of the group, verifying membership. Since zkSNARKs can only prove satisfaction of constraints involving arithmetic operations (+, -, and *), our check looks something like this:

signal temp;
temp <== (myHash - hash1) * (myHash - hash2);
0 === temp * (myHash - hash3);

Finally, by applying a MiMC hash on the message using user's secret key, we sign the message and return it. Having an output that depends on the specific message that the user wants to attest to prevents replay attacks; without this, the same proof could be used to attest to a different message.

component mimcAttestation = MiMCSponge(2, 220, 1);
mimcAttestation.ins[0] <== msg;
mimcAttestation.ins[1] <== secret;
mimcAttestation.k <== 0;
msgAttestation <== mimcAttestation.outs[0];

revealSigner ​

The second circuit proves that one's specific secret key was used to generate a group signature for a message, allowing a user to cryptographically reveal themselves. Circuit code here.

**Inputs:**
- myHash - MiMC hash of user's secret key (public)
- msg - the unsigned message to be validated (public)
- msgAttestation - the signed message to be validated (public)
- secret - User's secret key (private)

**Outputs:**
(none)

The circuit proves the following:

- msgAttestation == MiMC(msg, secret)
- myHash == MiMC(secret)

The circuit is similar to the message signing circuit. We first verify that the hash of the user's secret key is indeed the public key using MiMC. We then verify that the MiMC hash between the message and the user secret is the message attestation. This proves that the message was signed correctly by the right user.

denySigning ​

The last circuit allows users to deny ownership of a particular message. For instance, if an anonymous member sent something inappropriate, other members might want to deny the message to clear their name and single out the perpetrator.

This circuit is almost exactly the same as the message reveal circuit, except that instead of proving the user sent the message, we prove that the user did not send the message. The inputs are the same as the above circuit, while statements to prove are modified slightly:

- msgAttestation != MiMC(msg, secret)
- myHash == MiMC(secret)

See sample code here.

Protocol Augmentations ​

In the above section, we walked through a set of ZK circuits that enable a group of size 3 to anonymously sign messages & reveal/deny messages after they are posted. In this section, we consider possible protocol augmentations useful for productionalizing our construction, tying into how our ZK circuits could integrate with blockchain & decentralized backends.

Toggling Reveal and Deny ​

The ability for a particular user to easily deny that they sent a message might be undesirable. Consider the case where a malicious party wants to discover the identity of someone who sent a message and can credibly apply pressure/force to members of the signature group. They could systematically force members of the group to "deny" that they sent the message (for example threatening to fire people who don't submit a valid proof of denial), thereby discovering who sent the message.

To disable the ability for people to deny messages post-facto, we can remove the dependency of msgAttestation on secret in the sign circuit—for example, by setting msgAttestation := mimc(msg)^[3]. Note that this also removes the ability for people to reveal that they sent a message post-facto. An interesting exercise for the reader to think about is how to construct a circuit that allows a user to reveal that they sent a message, while removing the ability to deny authorship^[4].

Merkle Trees and Arbitrarily Large Groups ​

Another protocol add-on is to allow the circuit to check membership of arbitrarily large identity sets. With the approach outlined in the above section, we could try to increase the maximum identity set size by simply increasing the size of the public input array, or “compressing” all of the public keys into a single input by plugging them into a hash function that runs in the ZK proof. This is undesirable, however, because either the size of the input data or the computational complexity of the SNARK must scale linearly with the size of the array—even a relatively small cap of about 1000 public keys becomes hard to manage.

A common trick for verifying membership in large sets is to use a Merkle accumulator instead. By verifying inclusion in a Merkle tree instead of a hash list, we can scale our maximum set size. For an introduction to the Merkle tree data structure, see these two links.

Here's how our modified protocol would work:

• Given N public keys that a signer wants to create a group signature of, the signer would compute a Merkle tree (and root) containing the N keys, and publish the tree/root in a public location (a smart contract, IPFS, Github, etc.).
• When someone with a private secret to one of the N hashes wants to sign a message, they would use the published tree and their hashed secret to generate a Merkle proof corresponding to their secret. Note that this happens outside of the ZK circuit.
• Using the Merkle proof from above, the user would generate a ZK proof of set membership using a circuit with the following inputs & outputs:

**Inputs**:
- merkleRoot - merkle root of all hashes in identity set (public input)
- message - Message to be signed (public input)
- secret - User's secret key (private input)
- merkleProof - User-generated Merkle proof (private input)

**Outputs:**
- msgAttestation

The ZK proof would prove the following statements:

- myHash := mimc(secret)
- msgAttestation := mimc(msg, secret)
- merkleVerify(merkleProof, myHash, merkleRoot) == true // verify that merkleProof proves myHash is contained in merkleRoot

Notice that the inputs to the circuit are now of fixed size: merkleRoot is simply a single hash and merkleProof is an array of hashes equal to the depth of the Merkle tree. The number of hashes the Merkle tree can hold is equal to 2^d, where d is the depth of the tree, so even a tree of depth 30 is large enough for most practical purposes. Tornado Cash's implementation for a Circom circuit to verify Merkle proofs is here.

An application developer could snapshot an easily-auditable group (for example, “all ETH addresses owning a Cryptopunk as of timestamp X”), generate a Merkle tree for the group, publish the root on chain, and publish the tree on IPFS. Then, anyone would be able to generate and verify group signatures for this group by referencing this publicly-accessible data.

Trusted Group Managers ​

Some group signature constructions also define the notion of a group manager, who is granted extra permission by the protocol to de-anonymize signers, or to prove that a given group member did not produce a signature.

A group manager with these kinds of permissions can easily be instantiated in a zkSNARK group signature protocol by simply requiring protocol participants to include, as an additional output to the sign SNARK, their salted public key encrypted with a hardcoded group manager’s public key. To do this, the protocol developer would need to make use of ZK circuits for encryption and decryption.

Further Explorations ​

Centralized vs. Decentralized Backends ​

For the sake of demonstration, our proof of concept uses a centralized backend.

Using a centralized backend to store all the ZK proofs and messages has a number of tradeoffs—most obviously, allowing the server operator to censor undesirable messages. (In this case, we do plan to censor messages that are abusive). If we want censorship-resistance, then using a decentralized backend like a smart contract or peer-to-peer network might be desirable instead.

Note that the existence of a server which stores the signed messages does not affect the cryptographic properties of the signature scheme, since verification of group membership is done with inside the SNARK. The server does not know the identities of which user signed which message^[5]. The server also can’t generate “fake” proofs of membership in groups of which it is not a part.

Proofs of Property of Identity ​

An interesting corollary of enabling anonymous group signatures for groups of arbitrary size (using Merkle Accumulators as described above) is the possibility of proofs of properties of identity, rather than proofs of membership in arbitrary sets of individuals.

For example, zero-knowledge message boards could be configured to only allow posts from groups like these:

• Someone who currently owns a Cryptopunk
• Someone who used Ethereum in 2018 or earlier
• Someone who is a US Senator
• Someone who has at least 10k followers on Twitter

To make this happen, an application developer would maintain a Merkle root of all the hashes of e.g. current Cryptopunk holders, updated daily. Posts to the message board would require an accompanying ZK proof that the poster has control over a private address in that Merkle root, as described above.

Note that properties of identity cannot be enforced directly in the cryptography, since a proof can be constructed over any set of public keys. However, we can choose to only recognize signatures that correspond to a valid group as a matter of social convention. For example, a centralized backend could check that the Merkle tree a signature is constructed over is valid before saving posts to the database. A decentralized backend could implement the check on the client-side, simply hiding messages from groups deemed not-meaningful (e.g. a group signature from 50 senators plus one other public key).

This design also helps deter a number of adversarial scenarios. One example is for an adversary to write a message that could be plausibly attributed to another user, and post it under a group that includes their target(s)—something we saw happen with our early prototype. In this case, ZK forums could become a way for relatively anonymous griefers to roleplay as people with well-known reputations. However, reframing group signatures away from proof-of-membership towards proof-of-property-of-identity helps to mitigate this attack, since the signature is now proof that someone with this identity trait published a message, rather than someone in this group (additionally, it also helps to discourage the use of small or artificially constructed groups).

Blockchain-Based Extensions ​

These examples also hint at ways that blockchains can be used as credibly neutral ledgers for identity. For example, a smart contract could be configured to only accept messages from groups whose roots are whitelisted in an on-chain registry; such registries could be controlled by a DAO or governance token. A dapp could implement this pattern to mitigate spam or abuse from adversarial users.

ZK forums could be gated by NFT/asset ownership or DAO membership, and directories of real-world public keys could also be published on-chain and managed by an oracle (an individual or organization who monitors a list of real-world public figures).

Zero-Knowledge Polling and Voting ​

In our exploration, we’ve focused on zero-knowledge messaging, but a related family of applications is in voting and polling. Today, many colleges and professional organizations use Helios, a cryptographically verifiable anonymous voting system, to conduct elections. A SNARK-based version of Helios would allow for many alternate formulations and properties (e.g. MACI would make it impossible to prove that you voted a certain way after the fact).

The modularity of SNARKs opens up many new applications. What if neighborhood organizations had open polls where anyone could express their approval ratings for local governance across different issues? What if city council members and community leaders could be polled anonymously for their opinions throughout the year? While all of these are possible without zero-knowledge cryptography (using ring signatures and/or trusted servers), SNARKs reduce the barrier to experimentation significantly.

zkECDSA Group Signatures ​

One final note is that the hashing scheme used in our current construction requires users to generate and publish an application-specific public key, in our case, an arbitrary piece of private data hashed with the MiMC hash function. For purposes of interoperability, users should be able to sign messages with their existing public keys, such as their SSH key or Ethereum address.

This requires implementing the corresponding public-key signature scheme in the SNARK. One such scheme is the ECDSA curve used by Ethereum, which would make it possible for anonymous group signatures to be used with large, existing identity registries, such as the 227k addresses which currently hold Ethereum Name Service domains.

At the time we implemented our zero-knowledge message board, no such SNARK existed. However, there are now implementations for ECDSA signature verification in a SNARK in progress using multiple different languages and provers. We look forward to their release, which will open up the technology of anonymous group signatures and zero-knowledge cryptography to a far larger audience.

Links and Footnotes ​